Планирование решений в экономике
Рассмотрим основные элементы теории нечетких множеств. Пусть U— полное множество, охватывающее все объекты некоторого класса. Нечеткое подмножество F множества U, которое в дальнейшем будем называть нечетким множеством, определяется через функцию принадлежности mF (u), и Î U. Эта функция отображает элементы Ui, множества U на множество вещественных чисел отрезка [0,1], которые указывают степень принадлежности каждого элемента нечеткому множеству F.
Если полное множество U состоит из конечного числа элементов иi, i = 1, 2, ..., п, то нечеткое множество F можно представить в следующем виде:
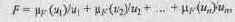
где "+" означает не сложение, а, скорее, объединение: символ "/" показывает, что значение mF относится к элементу, следующему за ним (а не означает деление на иi).
В случае, если множество U является непрерывным, F можно записать как интеграл:
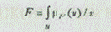
Нечеткие множества широко применяются для формализации лингвистических знаний. Рассмотрим для примера множество процентных ставок, предоставляемых банками по вкладам. Каким образом можно выделить подмножество высоких процентных ставок? В условиях динамично изменяющейся среды не всегда возможно точно ответить на этот вопрос, однозначно выделив множество высоких ставок. При использовании аппарата теории нечетких множеств решить такую задачу можно даже при отсутствии полной количественной информации об окружении.
Элементы теории нечетких множеств 2
Нечеткие операции отношения и свойства отношений
Нечеткие отношения
Свойства нечетких отношений
Многокритериальный выбор альтернатив на основе пересечения нечетких множеств
Многокритериальный выбор альтернатив на основе пересечения нечетких множеств 2
Многокритериальный выбор альтернатив на основе нечеткого отношения предпочтения
Многокритериальный выбор альтернатив 2
Многокритериальный выбор альтернатив 3
Многокритериальный выбор альтернатив 4
Многокритериальный выбор альтернатив с использованием правила нечеткого вывода
Многокритериальный выбор 2
Многокритериальный выбор 3
Многокритериальный выбор 4
Многокритериальный выбор альтернатив на основе аддитивной свертки
Многокритериальный выбор альтернатив на основе аддитивной свертки 2
Ранжирование альтернатив на множестве лингвистических векторных оценок
Ранжирование альтернатив 2
Ранжирование альтернатив 3
Банковское кредитование
Банковское кредитование 2
Банковское кредитование 3
Банковское кредитование 4
Банковское кредитование 5
Банковское кредитование 6
Выбор лучшего банка для размещения денежных средств физическим лицом
Выбор лучшего банка 2
Выбор лучшего банка 3
Выбор лучшего банка 4
Выбор лучшего банка 5
Выбор конкурентоспособного товара методом нечеткого отношения предпочтения
Выбор конкурентоспособного товара 2
Выбор конкурентоспособного товара 3
Выбор конкурентоспособного товара 4
Выбор конкурентоспособного товара 5
Выбор конкурентоспособного товара 6
Метод нечеткого логического вывода в задаче выбора фирмой кандидата на замещение вакантной должности бухгалтера
Метод нечеткого логического вывода 2
Метод нечеткого логического вывода 3
Метод нечеткого логического вывода 4
Метод нечеткого логического вывода 5
Метод нечеткого логического вывода 6
Метод нечеткого логического вывода 7
Метод нечеткого логического вывода 8
Метод нечеткого логического вывода 9
Метод нечеткого логического вывода 10
Метод нечеткого логического вывода 11
Метод нечеткого логического вывода 12
Метод нечеткого логического вывода 13
Метод нечеткого логического вывода 14
Метод нечеткого логического вывода 15
Метод нечеткого логического вывода 16
Выбор фирмой стратегии расширения доли рынка методом аддитивной свертки
Выбор фирмой стратегии расширения 2
Выбор фирмой стратегии расширения 3
Выбор фирмой стратегии расширения 4
Выбор предприятия для кредитования методом лингвистических векторных оценок
Выбор предприятия для кредитования 2
Выбор предприятия для кредитования 3
Выбор предприятия для кредитования 4
Сравнительный анализ различных методов принятия решений
Характеристика критериев
Описание альтернатив
Решение задачи методом максиминной свертки
Решение задачи с использованием метода отношений предпочтения
Решение задачи с использованием метода отношений предпочтения 2
Решение задачи с применением нечеткого логического вывода
Решение задачи с применением нечеткого логического вывода 2
Решение задачи с применением нечеткого логического вывода 3
Решение задачи методом аддитивной свертки
Решение задачи методом аддитивной свертки 2
Решение задачи методом анализа иерархий
Сравнение полученных результатов
Сравнение полученных результатов 2
Контрольные вопросы и задания
Литература
Три манифеста баз данных ретроспектива и перспективы
В период с 1989 по 1995 гг. авторские группы, включающие известных специалистов в области баз данных, подготовили и опубликовали три документа, которые отражали точки зрения авторов относительно перспектив развития технологии баз данных. С легкой руки авторов хронологически первого документа эти документы получили название манифестов, что, в общем-то, отражало их суть: в каждом из документов провозглашался набор идей и требований, на которых, по мнению авторов, должны были базироваться системы баз данных следующего поколения.Финансы
И снова про деньги, но под другим именем - финансы. Люди научились крутить вертеть любые цифры так что с одной стороны можно показать вам офигенную прибылищу, а с другой - голубчик, да вы нищий. Вс эта байда называется самиы разными словами, но чаще всего говорят про анализ.Финансы - Активы
Финансы - Акции
Финансовый анализ
Финансовая деятельность
Диагностика финансов
Задачи финансов
Финансы - Зарплата
Финансовые инвестиции
История финансов
Корпоративные финансы
Методы анализа финансов
Страхование финансов
Структура финансов
Теория финансов
Финансовое моделирование
Финансовая модель рынка
Финансы как наука
Финансы - Несостоятельность
Финансы - Облигации
Финансы организации
Основа финансов
Финансовая отчетность
Финансовая оценка
Финансовое планирование
Финансовые показатели
Учебник по финансам
Финансовое состояние
Финансы - Форварды
Финансовая хоз. деятельность
Портфельное инвестирование
Финансовые потоки
Финансы предприятия
Финансовая прибыль
Финансовый результат
Финансовый риск
Финансы России
Финансовый рынок
Финансовая система
Финансовый софт
Финансовая стратегия
Управление финансами
Финансы - Сложные проценты
Финансы - Имитационные модели
