Многокритериальный выбор альтернатив с использованием правила нечеткого вывода

 

Рассмотрим метод многокритериального выбора альтернатив на основе композиционного правила агрегирования описаний альтернатив с информацией о предпочтениях лица, принимающего решение, которые заданы в виде нечетких суждений [2].

Сущность метода, на основе которого реализована компьютерная система, заключается в следующем. Пусть U — множество элементов, А — его нечеткое подмножество, степень принадлежности элементов к которому есть число из единичного интервала [0, 1]. Подмножества Aj являются значениями лингвистической переменной X.

Допустим, что множество решений характеризуется набором критериев х1, х2, ..., xp, т.е. лингвистических переменных, заданных на базовых множествах и1, и2, .... up соответственно. Например, переменная х1 "качество управления" может иметь значение НИЗКОЕ, а переменная х2 "стоимость" — значение ХОРОШЕЕ и т. д. Набор из нескольких критериев с соответствующими значениями характеризует представления лица, принимающего решение, об удовлетворительности альтернативы. Переменная S "удовлетворительность" также является лингвистической.

 

Ниже приведен пример высказывания :

d1: "Если x1 = НИЗКОЕ и x2 = ХОРОШЕЕ, то S = ВЫСОКАЯ". В общем случае высказывание d1 имеет вид:

 

d1: "Если x1 = А1, и x2 = А2i и ... хр = Арi то S = Вi".      (4.1)

 

Обозначим пересечение (x1 = А1i Ç x2 = А2i Ç... хр = Арi) через х = Аi.

Операции пересечения нечетких множеств соответствует нахождение минимума их функций принадлежности:

 

 

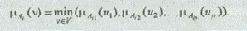
Здесь V= U1 ´U2 ´...Up;

v = (u1, и2 ..., up); mAij (uj) — значение принадлежности элемента и, нечеткому множеству Аij.