Отношения мер сходства включения и иерархии

 

Отношения мер сходства (различия), включения и иерархии позволяют при обработке множеств исследуемых объектов выявлять наиболее интересные закономерности строения анализируемых множеств. В общем случае под отношением понимается пара <А, М>, где М— множество, на котором отношение определено, а А — подмножество пар М x М, для которых это отношение выполнено. Множество М называется областью задания отношения А.

Отношения мер сходства и иерархии исследуются на основе матриц сходства множества рассматриваемых объектов, а отношения мер различия и включения исследуются на основе матриц мер различия и включения. При этом матрицы сходства и различия по определению соответствующих мер обладают свойством симметрии относительно главной диагонали, а матрицы мер включения таким свойством не обладают.

 

Отношения сходства, различия и включения, порождаемые соответствующими мерами, определяются следующим образом:

 

 

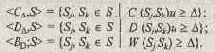
Здесь j, k Î J; СD, DD, BD —соответственно отношения сходства, различия и включения;

D— некоторое произвольное число (0 £ D  £ 1,0 для отношения сходства и включения).

 

Записи Sj СD Sk и Sj BD Sk означают соответственно то, что Sj и Sk находятся в отношении "D-сходства" и "D-банальности".

 

Отношение "банальности" или "экзотичности" порождается мерой включения.

При этом запись Sj BD Sk означает, что описание Sj "банальнее" Sk при пороге D.