Мультипликативная целевая функция
Найти подмножество SÎ W, для элементов которого
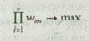
Вопрос о том, какая из этих двух средневзвешенных более адекватно отражает поведение человека, принимающего решение с учетом не одного, а нескольких показателей, был предметом научной дискуссии Галилея с Ноццолино еще в 17в. (Галилей отдавал предпочтение среднегеометрическому, а Ноццолино — среднеарифметическому). С тех пор многие ученые — специалисты в области статистики, психофизиологии и другие высказывали различные теоретические доводы в пользу каждой из этих двух средневзвешенных. В различных областях науки и практики аддитивный показатель качества в виде средневзвешенной арифметической используется гораздо чаще, чем другие виды средневзвешенных (например, среднегеометрическая). Однако использование аддитивного показателя качества требует, чтобы между относительными показателями любых свойств существовала независимость по предпочтению.
Решение второй задачи сводится к поиску в морфологическом множестве подмножества вариантов систем, наиболее сходных с поисковым заданием.
Целевая функция в этой задаче определяется следующим образом: найти подмножество SÎ W, для элементов которого
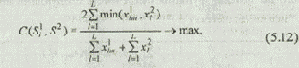
где С(Si1, S2) — мера сходства между описанием рассматриваемого варианта системы Si1 и описанием поискового задания S2;
x1lm, x2l — числовые значения критериев качества, характеризующие соответственно рассматриваемый вариант системы и поисковое задание;
L — может иметь два значения и определять либо число обобщенных функциональных подсистем, либо число критериев качества, которыми на количественном уровне охарактеризованы описания Si1 и S2;
т — порядковый номер альтернативы в строке морфологической матрицы.
